液滴

最終更新日時: 2025年08月25日 12:57

TODOs

• nothing

TODOs

• nothing

ステイタス

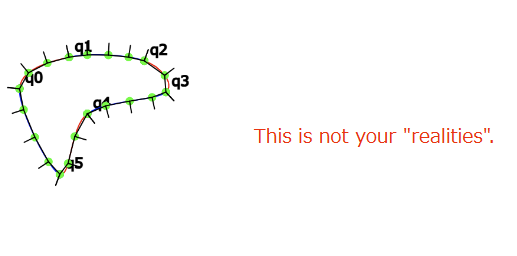
• このプログラム自体は完成したがこの結果をどう適用するのかまだ不明

はじめに

• 目的：液体の界面のような曲線を描く
• 構成：index.htmlの中に一つだけ呼び出されるsketch.jsというファイルを出力する
• 技術：生成するjavascriptはp5jsを利用、数学的処理は全てMathの関数を利用
• アルゴリズム：ランダムな点をスプライン曲線で滑らかにつなぐ

詳細なプログラムの動作

• キャンバスの大きさを決定
  • 定数WIDTH=400, HEIGHT=400で定義
• キャンバスの大きさの矩形内に乱数で頂点をＮ個生成。
  • $k$番目の点を$p(k,t)$とする。$0<=k<=N-1$
  • $N$は偶数である
  • $N=6$として定数定義
  • 頂点はキャンバスの左右上下の一定の幅FRAME値を見ごろとして取る
  • $FRAME=30$として定数定義
• これらの点を並びなおして新たに$q(k,t)$を以下のルールで生成する
  • 全ての点を通る多角形を構成する順番にする
  • 隣り合う$q(k,t),q(k+1,t)$で線分を描く$q(N,t)$に対しては$q(N,t),q(0,t)$の間に線分を描く
  • これらの線分は交差しないことが条件で$q(k,t)$を生成する

function orderPoints() {
    let { centerX, centerY } = points.reduce((acc, p) => {
        acc.centerX += p.x;
        acc.centerY += p.y;
        return acc;
    }, { centerX: 0, centerY: 0 });

    centerX /= points.length;
    centerY /= points.length;

    points.sort((a, b) => {
        return Math.atan2(a.y - centerY, a.x - centerX) - Math.atan2(b.y - centerY, b.x - centerX);
    });
}

Code 01: reduceを使って改善された点の並べ替え

• $q(k,t)$を描画する

  • 点は$circle()$で半径$R$として描画する
    • stroke, fillともに色は黒とする
    • $R=3$として定数定義する
  • 全ての$q(k,t)$の点は右上に$q(k)$として名前をテキストで描画する
    • 文字色は黒色とする

• q(k,t),q(k+1,t)をつなぐ線分を破線で描く

  • 線分の色は黒色とする

• $q(k,t),q(k+1,t)$,$q(k+2,t)$の3点を通る曲線を描く

  • 曲線はスプライン曲線とする
  • $k$は0から$N-1$まで1づつ変化させる
  • ただし$k=N-1$の時,$k+1=0, k+2=1$とする
  • 線の色は$k$なら赤とするそれ以外は青とする
  • $q(k+1,t),q(k+2,t)$の間には、$q(k,t),q(k+1,t),q(k+2,t)$を通る曲線と$q(k+1,t),q(k+2,t),q(k+3,t)$を通る二本の曲線が異なる色で異なる曲線として描かれる
  • この曲線は、下記のようなアルゴリズムで達成する

  function drawCurves() {
    for (let i = 0; i < orderedPoints.length; i++) {
        let p0 = orderedPoints[i];
        let p1 = orderedPoints[(i + 1) % orderedPoints.length];
        let p2 = orderedPoints[(i + 2) % orderedPoints.length];
        let p3 = orderedPoints[(i + 3) % orderedPoints.length];

        noFill();
        stroke(i % 2 === 0 ? 'blue' : 'red');

        // Catmull-Romスプライン
        beginShape();
        curveVertex(p0.x, p0.y);
        curveVertex(p1.x, p1.y);
        curveVertex(p2.x, p2.y);
        curveVertex(p3.x, p3.y);
        endShape();
    }
}

Code 02: 曲線描画

• 各区間の曲線上に均等に補間点$r(m)$を生成する。
• 補間点の数は$M(k,k+1)$とする
• $M(k,k+1)$の保管点の密度は全閉曲線で一定の$c$とする
• Catmull-Romスプラインの点を補間して新しい点列$r(m)$を生成する。
• このようにして得られる曲線を$Ｑ$とする
• 曲線Ｑは閉曲線である
• この閉曲線は閉曲線内に

次のステップ

• 目標：

初期条件の設定:

シミュレーション領域の定義

• 2次元の計算領域を設定
• 格子点数と格子間隔を決定
• シミュレーション単位時間を決定

液滴の初期形状の定義

• レベルセット関数$\phi(x,y,z)$を用いて液滴の初期形状を表現
• $\phi< 0$が液滴内部、$\phi> 0$が外部、$\phi = 0$が界面を表す

初期速度場の設定

• 全領域で初期速度$u(x,y,z)$を$(0,0,0)$と定義

物性値の設定

• 液滴と周囲流体の密度$ρ$、粘性$μ$、表面張力係数$σ$を設定

境界条件の設定

計算領域の境界における速度と圧力の条件を指定

時間発展のメインループ:

• 各時間ステップ$\delta t$ごとに以下の操作を繰り返す

レベルセット関数の更新

• レベルセット方程式を解く

$$\frac{\partial\phi}{\partial t} + u \cdot \nabla \phi = 0$$

• いずれかの数値スキームを用いて離散化
  • ENO(Essentially Non-Oscillatory)
  • WENO (Weighted Essentially Non-Oscillatory)
  • MUSCL (Monotonic Upstream-Centered Scheme for Conservation Laws) 法
• 必要に応じて再初期化を行い、符号付き距離関数の性質を保持

用語説明（このセクションは指示文ではなく人間が読むためのセクションである)

• ステンシル

  • 計算点の周りの格子点のグループのこと。
  • 「三点ステンシル」は、注目している点とその左右の点を含む3つの点のグループを指す

• 分割差分

  • 隣接する点間の値の変化率のこと
  • 例えば、$f(x+h) - f(x)$を $h$で割ったものが分割差分の一例

• 数値流束

  • 数値計算において、物理量（質量、運動量など）の流れを表す量

• データ勾配 データの変化の度合いを表す

  • 簡単に言えば、グラフの傾きのようなものです。

• 界面値

  • セル（計算領域を分割した小さな領域）の境界での値のことです。

• ENO法は、急激な変化がある領域でも、振動（数値計算上の不自然な揺れ）を抑えつつ高い精度を保つ方法です。複数の可能なステンシル（計算に使う点のグループ）から、最も「滑らか」なものを選びます。ここで「滑らか」とは、値の変化が緩やかであることを意味します。この方法により、急激な変化の近くでも安定した計算が可能になります。

• WENO法はENO法を発展させたものです。ENO法が一つのステンシルを選ぶのに対し、WENO法は複数のステンシルを重み付けして使います。各ステンシルの「滑らかさ」に基づいて重みを決定し、より滑らかなステンシルに大きな重みを与えます。これにより、ENO法よりもさらに高い精度を達成できます。

• MUSCL法は、セル（計算領域の小さな区画）内での値の分布を直線で近似する方法です。各セルの境界（界面）での値を、セル中心の値とデータの勾配（変化の度合い）を使って推定します。ただし、急激な変化がある領域では、推定値が大きく振動するのを防ぐため、「リミッター関数」という特殊な関数を使って勾配を制限します。これにより、安定性と精度のバランスを取ります。 これらの方法の共通点は、急激な変化（例えば、衝撃波）を含む流れを正確にシミュレーションしようとする点です。違いは主に以下の通りです：

ENO法：複数の候補から最も適切なステンシルを選択 WENO法：複数のステンシルを重み付けして使用（より高精度だが計算コストが高い） MUSCL法：セル内の値の分布を直線で近似し、リミッター関数で制御（比較的シンプルで計算コストが低い）

b. 速度場の予測

ナビエ・ストークス方程式の移流項と粘性項を解く $u* = u? + Δt[-（u?・∇）u? + ν∇2u? + g]$（$g$は重力等の外力） 適切な離散化法（例: 中心差分、風上差分）を用いる

c. 圧力場の計算

圧力ポアソン方程式 $∇2p = ρ/Δt ∇・u*$を解く 適切な解法（例: SOR法、共役勾配法）を用いる 境界条件を考慮

d. 速度場の修正

$u??1 = u* - Δt/ρ ∇p$ これにより、非圧縮条件 $∇・u = 0$を満たす

e. 界面の取り扱い

Ghost Fluid Method等を用いて、密度・粘性の不連続性を考慮 表面張力の計算: $F_σ = σκδ(φ)n$（$κ$は曲率、$n$は法線ベクトル）

f. 物理量の更新

新しい速度場$u??1$と圧力場$p??1$を保存

g. 可視化データの出力

必要に応じて、速度場、圧力場、液滴形状等のデータを出力

後処理:

シミュレーション結果の解析 グラフィカルな表示（例: 液滴形状の時間変化、速度ベクトル場の可視化）

注意事項:

数値安定性を確保するため、クーラン条件等を考慮してΔtを適切に選択する 界面の急激な変形や分裂・合体に対応できるよう、適応的な格子細分化を検討する 並列計算の導入を検討し、計算効率を向上させる

これらの手順を踏むことで、液滴の時間発展をシミュレーションするプログラムを構築できます。各ステップの具体的な実装方法は、使用するプログラミング言語や数値ライブラリによって異なりますが、この指示文は一般的なアプローチを提供しています。

# sketch.js for ekiteki

const WIDTH = 200;
const HEIGHT = 200;
const N = 6;   // 元の点の数
const FRAME = 30;
const R = 3;
const TOTAL_POINTS = 20; // 補完する点の総数
let points = [];
let orderedPoints = [];
let rPoints = [];

function setup() {
    createCanvas(WIDTH, HEIGHT);
    generateRandomPoints();
    orderPoints();
    console.log(`Generated ${points.length} points:`, points); // 生成されたポイントのデバッグ
    console.log(`Ordered ${orderedPoints.length} points:`, orderedPoints); // ソートされたポイントのデバッグ
    drawPolygon();
    drawCurves();
    generateInterpolatedPoints();
    drawInterpolatedPoints();
    console.log('Interpolated points:', rPoints); // 補間点のデバッグ
    drawLiquidInterpolatedPoints();
}

function draw() {
    noLoop();
}

function generateRandomPoints() {
    points = []; // ポイントのリセット
    for (let i = 0; i < N; i++) {
        let x = random(FRAME, WIDTH - FRAME);
        let y = random(FRAME, HEIGHT - FRAME);
        points.push(createVector(x, y));
    }
    points.forEach(p=>{
  console.log(`${p.toString()}`);
    });
}

function orderPoints() {
    let centerX = 0;
    let centerY = 0;
    points.forEach(p => {
        centerX += p.x;
        centerY += p.y;
    });
    centerX /= points.length;
    centerY /= points.length;

    points.sort((a, b) => {
        let angleA = atan2(a.y - centerY, a.x - centerX);
        let angleB = atan2(b.y - centerY, b.x - centerX);
        return angleA - angleB;
    });

    orderedPoints = points.slice();
}

function drawPolygon() {
    background(255); // キャンバスをリセット
    stroke(0);
    fill(0);
    for (let i = 0; i < orderedPoints.length; i++) {
        let p = orderedPoints[i];
        ellipse(p.x, p.y, R * 2, R * 2); // 各点に半径Rの円を描画
        text(`q${i}`, p.x + 5, p.y - 5); // 各点の右上にテキストを描画
        let next = orderedPoints[(i + 1) % orderedPoints.length];
        //line(p.x, p.y, next.x, next.y); // 各点を結ぶ線を描画
    }
}

function drawCurves() {
    for (let i = 0; i < orderedPoints.length; i++) {
        let p0 = orderedPoints[i];
        let p1 = orderedPoints[(i + 1) % orderedPoints.length];
        let p2 = orderedPoints[(i + 2) % orderedPoints.length];
        let p3 = orderedPoints[(i + 3) % orderedPoints.length];


        noFill();
        stroke(i % 2 === 0 ? 'blue' : 'red');

        // Catmull-Romスプライン

        beginShape();
        curveVertex(p0.x, p0.y);
        curveVertex(p1.x, p1.y);
        curveVertex(p2.x, p2.y);
        curveVertex(p3.x, p3.y);
        endShape();

    }
}

function calculateSegmentLength(p0, p1, p2, p3, t) {
    let dx = curveTangent(p0.x, p1.x, p2.x, p3.x, t);
    let dy = curveTangent(p0.y, p1.y, p2.y, p3.y, t);
    return sqrt(dx * dx + dy * dy);
}

function integrateLength(p0, p1, p2, p3, steps) {
    let length = 0;
    for (let i = 0; i < steps; i++) {
        let t0 = i / steps;
        let t1 = (i + 1) / steps;
        let len = (calculateSegmentLength(p0, p1, p2, p3, t0) + calculateSegmentLength(p0, p1, p2, p3, t1)) / 2;
        length += len * (t1 - t0);
    }
    return length;
}

function generateInterpolatedPoints() {
    rPoints = [];
    let totalLength = 0;
    let lengths = [];

    // 各セグメントの長さを計算
    for (let i = 0; i < orderedPoints.length; i++) {
        let p0 = orderedPoints[i];
        let p1 = orderedPoints[(i + 1) % orderedPoints.length];
        let p2 = orderedPoints[(i + 2) % orderedPoints.length];
        let p3 = orderedPoints[(i + 3) % orderedPoints.length];
        let length = integrateLength(p0, p1, p2, p3, 100);
        lengths.push(length);
        totalLength += length;
    }

    // 各セグメントに補間点を分配
    for (let i = 0; i < orderedPoints.length; i++) {
        let numPoints = Math.round(TOTAL_POINTS * (lengths[i] / totalLength));
        let p0 = orderedPoints[i];
        let p1 = orderedPoints[(i + 1) % orderedPoints.length];
        let p2 = orderedPoints[(i + 2) % orderedPoints.length];
        let p3 = orderedPoints[(i + 3) % orderedPoints.length];

        for (let j = 0; j <= numPoints; j++) {
            let t = j / numPoints;
            let x = curvePoint(p0.x, p1.x, p2.x, p3.x, t);
            let y = curvePoint(p0.y, p1.y, p2.y, p3.y, t);
            let tangent = createVector(curveTangent(p0.x, p1.x, p2.x, p3.x, t), curveTangent(p0.y, p1.y, p2.y, p3.y, t));
            let normal = createVector(tangent.y, -tangent.x).normalize().mult(10); // 垂直な外向きベクトルを反転
            rPoints.push({ position: createVector(x, y), normal: normal });
        }
    }
}

function drawInterpolatedPoints() {
    stroke(0, 255, 0);
    fill(0, 255, 0);
    for (let i = 0; i < rPoints.length; i++) {
        let p = rPoints[i].position;
        ellipse(p.x, p.y, R * 2, R * 2); // 各補完点に半径Rの円を描画
    }

    stroke(0);
    for (let i = 0; i < rPoints.length; i++) {
        let p = rPoints[i].position;
        let n = rPoints[i].normal;
        line(p.x, p.y, p.x + n.x, p.y + n.y); // 接線の垂直外向きベクトルを描画
    }
}

function drawLiquidInterpolatedPoints() {
    for (let i = 0; i < rPoints.length; i++) {
        let p = rPoints[i].position;
        let q = rPoints[(i+1>=rPoints.length ? 0 : i+1)].position;
  line(p.x,p.y,q.x,q.y);
    }
}

function curveTangent(a, b, c, d, t) {
    return 3 * (1 - t) * (1 - t) * (b - a) + 6 * (1 - t) * t * (c - b) + 3 * t * t * (d - c);
}