(r)補間法
最終更新日時: 2025年08月25日 12:57
補間法というのは基本的に全ての点を通る関数を得ることである。 何次の導関数まで滑らかにつなげるかは各補間の方式で異なる。 また、最小二乗法などの近似法という類似の概念は、 与えられた点を通るとは限らず、トレンドを表現する方法。
| 手法 | 特徴 | 導関数の連続性 |
|---|---|---|
| スプライン | 三次のスプライン多項式を利用 | 1,2次導関数が連続 |
| エルミート | エルミート多項式を基底に利用 | 1次導関数が連続 |
| ラグランジュ | 複数の補間点で単一の関数を定義。条件により端点が振動 | 一つのN次補間関数なので微分可能 |
| 双曲線 | 2点間の双曲線は一意に定まらない | すべての導関数が連続(極を含まない区間で) |
| 線形 | 2点間を直線で結ぶ | 非連続 |
1. エルミート補間
Section titled “1. エルミート補間”エルミート多項式の基底関数を利用して補間関数を見出す。 一つの補完する区間で2点 , と導関数 を初期条件とする。 エルミート補間はラグランジュ補間の拡張であり、導関数の情報を加味することで、補間精度や滑らかさを向上させる。ラグランジュ補間は、導関数情報がない場合の特別なケースと見なせる。
- 単一区間を見たときに
- 及び補間点の一次微分の値は:
補間関数:
基底関数:
ここで、
点 (1, 2), (2, 3), (3, 5)の3点を例にとる
(1,2),(2,3)間の補間関数は
- 導関数が なので、補間式は次に簡略化:
- を代入し、以下を得る
(2,3),(3,5)間の補間関数は
- 導関数が なので、補間式は次に簡略化:
- を代入し、以下を得る
よって、
2. ラグランジュ補間
Section titled “2. ラグランジュ補間”与えられた 点 を一つのn+1次曲線で補間する。
補間関数:
基底関数:
計算例(1)
Section titled “計算例(1)”点 (1, 2), (2, 3), (3, 5)の3点を例にとる。
- :
- :
- :
以上より補間式は、
計算例(2)
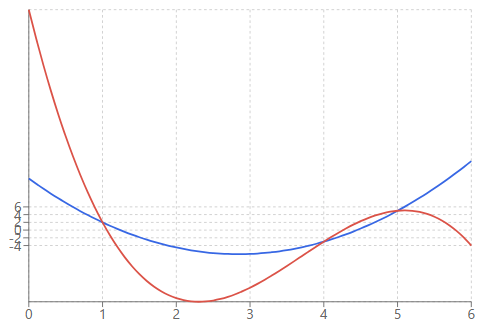
Section titled “計算例(2)”- (1, 2), (4, -3), (5, 5)の3点について補間した曲線を青色
- (1, 2), (4, -3), (5, 5),(6,-4)の3点について補間を赤色
Runge現象について
Section titled “Runge現象について”等間隔な点での高次多項式補間において、補間点の間で大きな振動が発生する現象です 特に、区間の端部近くで振動が顕著になります 補間点の数を増やしても改善されず、むしろ振動が悪化する場合があります
なぜ起こるのか
Section titled “なぜ起こるのか”高次の多項式補間では、すべての補間点を通過するために多項式の次数が上がります 高次の多項式は本質的に振動的な性質を持ちます 特に区間の端では、他の点を通るための「代償」として大きな振動が発生します
例えば、関数 f(x) = 1/(1 + 25x2) を [-1,1] 区間で等間隔な点を使って補間する場合:
- この関数自体は滑らかで振動のない関数です
- しかし、等間隔な点で高次のラグランジュ補間を行うと、端部で大きな振動が発生します 補間点を増やすと、振動はさらに激しくなります
Runge現象を回避または軽減するための方法がいくつかあります:
- チェビシェフ点の使用
- 等間隔点の代わりに、区間の端部で密になるように分布させたチェビシェフ点を使用すると端部での振動を抑制できる
2.スプライン補間の使用
- 高次の多項式の代わりに、低次の区分的多項式を使用する。各区間で3次や4次程度の多項式を使うため、振動が抑制される
なぜラグランジュ補間で特に問題になるのか
Section titled “なぜラグランジュ補間で特に問題になるのか”ラグランジュ補間は、与えられたすべての点を通る単一の多項式を構築する。 点の数が増えると多項式の次数も上がり、振動が増幅される可能性がある。 特に等間隔点を使用する場合、この問題が顕著になる。
これが、冒頭の表で「ラグランジュ補間では大区間でRunge現象の可能性がある」 と記載されている理由です。ただし、適切な点の選び方(チェビシェフ点など)や区間の分割を行えば、この問題は軽減できます。
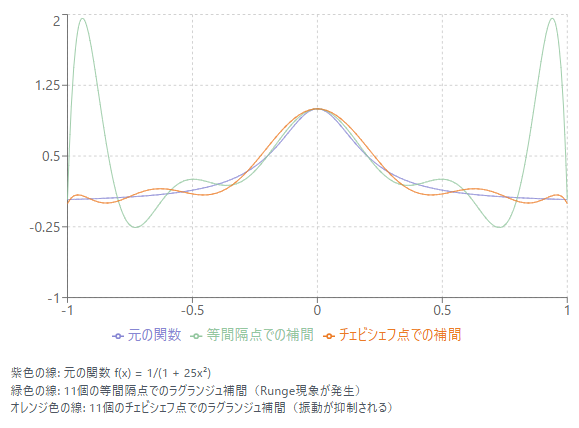
可視化して確認してみる
Section titled “可視化して確認してみる”11個の等間隔な点でのラグランジュ補間したグラフが緑色の線である。 区間の端部で大きな振動が発生しており、これをRunge現象と呼び、 確かに補間点の間でも望ましくない振動が見られる
3. スプライン補間
Section titled “3. スプライン補間”各区間 毎に3次多項式を用いる補間法。
各区間の補間関数:
係数 は、値と1次・2次導関数の連続性、および境界条件を用いて決定。
1. 前提条件
Section titled “1. 前提条件”n+1個のデータ点 が与えられているとします。
2. 連続性条件
Section titled “2. 連続性条件”以下の条件を満たす必要があります:
- 位置の連続性:
- 1次導関数の連続性:
- 2次導関数の連続性:
3. 2次導関数を用いた表現
Section titled “3. 2次導関数を用いた表現”2次導関数の連続性から
各点での2次導関数の値を とおきます。 区間の長さを とします。
5. 三重対角行列の形成
Section titled “5. 三重対角行列の形成”これを行列形式で書くと:
6.トーマスのアルゴリズム
Section titled “6.トーマスのアルゴリズム”三重対角行列を解く問題を次の形で表します:
ここで:
- は対角成分
- はそれぞれ下対角・上対角成分
- は右辺ベクトル
目的は、 を効率的に求めることです。
アルゴリズムの手順
Section titled “アルゴリズムの手順”ステップ1: 前進消去
Section titled “ステップ1: 前進消去”三重対角行列の下対角成分 をゼロにして、簡略化します。
-
対角成分を更新:
-
右辺ベクトルを更新:
計算は から まで進めます。
ステップ2: 後退代入
Section titled “ステップ2: 後退代入”前進消去で得られた三角行列を用いて、 を逆順に計算します。
-
最後の未知数を計算:
-
上から順に再帰的に計算:
計算は から まで進めます。
- 計算量:
- 効率的: 行列サイズが大きい場合でも高速に解ける。
- 制約: 三重対角行列にのみ適用可能。
トーマスのアルゴリズムは、三重対角行列の特殊な構造を活用し、効率的に線形方程式を解く方法です。前進消去と後退代入の2ステップで計算します。この手法は、三次スプライン補間のような問題に適用されます。
6. スプライン係数の計算
Section titled “6. スプライン係数の計算”三重対角行列を解いて が得られたら、各区間 の係数は以下のように計算できます:
これにより、各区間での三次スプライン関数が完全に決定されます。得られる補間関数は:
- 各データ点を通り
- 隣接する区間で1次導関数まで連続
- 2次導関数も連続
という性質を持ちます。
7. 実装上の注意点
Section titled “7. 実装上の注意点”-
境界条件の設定
- 自然スプライン:両端で2次導関数を0とする()
- 周期的スプライン:始点と終点で1次・2次導関数が一致
- Not-a-knot:両端の2つの区間で3次導関数が一致
-
三重対角行列の解法
- トーマスのアルゴリズム(LU分解の特殊ケース)を使用
- 計算量は O(n)
-
数値安定性
- 等間隔でないデータ点の場合も適切に処理
- 丸め誤差の影響を最小限に抑える必要あり
4. 双曲線補間
Section titled “4. 双曲線補間”双曲線の形を用いた補間法。
補間関数:
与えられた点を代入して、係数 を求める。
- 補間区間に極を含む場合、関数値が発散するため適切な補間ができないため 双曲線補間を利用する時は、補間区間に極を含まないように注意する必要がある
- 二点間の補間のため、4変数は定まらず2変数が残るので補間関数には自由度が残る
- 極とは、関数値が無限大に発散する点のことである。 下記の関数を例にとって極とその周辺のふるまいを説明する。
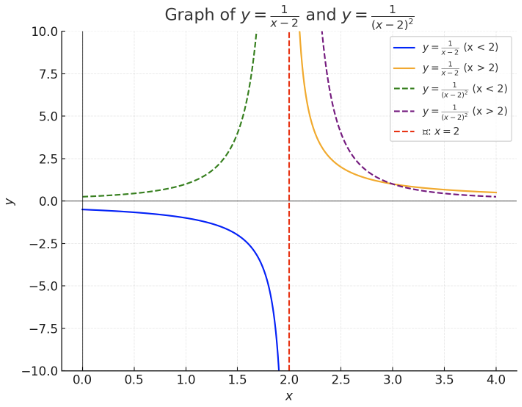
- この例では x = 2 が極で分母が0になる点で発生する。
- 極を含まない区間では、関数は無限回微分可能だが、極の近傍では導関数も無限大に発散する。
5. 線形補間
Section titled “5. 線形補間”2点間を直線で結ぶ簡単な補間法。
補間関数:
点 (1, 2), (2, 3), (3, 5)の3点を例にとる
(1,2)と(2,3)間の式は、
(2,3),(3,5)間の式は、
サンプルコード
Section titled “サンプルコード”1. エルミート補間
Section titled “1. エルミート補間”function hermiteInterpolation(x: number, x0: number, x1: number, y0: number, y1: number, y0Prime: number, y1Prime: number): number { const t = (x - x0) / (x1 - x0); const h0 = 1 - 3 * t * t + 2 * t * t * t; const h1 = 3 * t * t - 2 * t * t * t; const h2 = t - 2 * t * t + t * t * t; const h3 = -t * t + t * t * t;
return h0 * y0 + h1 * y1 + h2 * (x1 - x0) * y0Prime + h3 * (x1 - x0) * y1Prime;}2.エルミート補間
Section titled “2.エルミート補間”function lagrangeInterpolation(x: number, points: { x: number, y: number }[]): number { let result = 0;
for (let i = 0; i < points.length; i++) { let term = points[i].y; for (let j = 0; j < points.length; j++) { if (i !== j) { term *= (x - points[j].x) / (points[i].x - points[j].x); } } result += term; }
return result;}3.1.線形スプライン補間
Section titled “3.1.線形スプライン補間”function linearSplineInterpolation(x: number, points: { x: number, y: number }[]): number { for (let i = 0; i < points.length - 1; i++) { const x0 = points[i].x, y0 = points[i].y; const x1 = points[i + 1].x, y1 = points[i + 1].y;
if (x >= x0 && x <= x1) { return y0 + (y1 - y0) * (x - x0) / (x1 - x0); } }
throw new Error("x is out of the range of the provided points.");}- CubicSpline クラス:
- スプライン係数 a,b,c,d を計算し保存します。
- calculateCoefficients メソッド:
- 3次スプラインの係数を計算します。h,α,l,μ,z を用いて b,c,d を決定します。
- interpolate メソッド:
- 指定された x の値に基づいて補間を実行します。
3.2. 三次のスプライン補間
Section titled “3.2. 三次のスプライン補間”// 3次スプライン補間class CubicSpline { private x: number[]; private y: number[]; private a: number[]; // 各区間の定数項 private b: number[]; // 各区間の一次係数 private c: number[]; // 各区間の二次係数 private d: number[]; // 各区間の三次係数
constructor(x: number[], y: number[]) { if (x.length !== y.length || x.length < 2) { throw new Error("x と y は同じ長さで、少なくとも2点必要です。"); } this.x = x; this.y = y; this.a = [...y]; this.b = []; this.c = []; this.d = []; this.calculateCoefficients(); }
private calculateCoefficients() { const n = this.x.length - 1; const h: number[] = []; const alpha: number[] = new Array(n).fill(0);
for (let i = 0; i < n; i++) { h[i] = this.x[i + 1] - this.x[i]; if (h[i] <= 0) { throw new Error("x は単調増加でなければなりません。"); } }
for (let i = 1; i < n; i++) { alpha[i] = (3 / h[i]) * (this.a[i + 1] - this.a[i]) - (3 / h[i - 1]) * (this.a[i] - this.a[i - 1]); }
const l: number[] = new Array(n + 1).fill(1); const mu: number[] = new Array(n + 1).fill(0); const z: number[] = new Array(n + 1).fill(0);
for (let i = 1; i < n; i++) { l[i] = 2 * (this.x[i + 1] - this.x[i - 1]) - h[i - 1] * mu[i - 1]; mu[i] = h[i] / l[i]; z[i] = (alpha[i] - h[i - 1] * z[i - 1]) / l[i]; }
const c: number[] = new Array(n + 1).fill(0); const b: number[] = new Array(n).fill(0); const d: number[] = new Array(n).fill(0);
for (let j = n - 1; j >= 0; j--) { c[j] = z[j] - mu[j] * c[j + 1]; b[j] = (this.a[j + 1] - this.a[j]) / h[j] - h[j] * (c[j + 1] + 2 * c[j]) / 3; d[j] = (c[j + 1] - c[j]) / (3 * h[j]); }
this.b = b; this.c = c.slice(0, n); this.d = d; }
public interpolate(x: number): number { const n = this.x.length - 1; let i = n - 1; for (let j = 0; j < n; j++) { if (x >= this.x[j] && x <= this.x[j + 1]) { i = j; break; } }
const dx = x - this.x[i]; return this.a[i] + this.b[i] * dx + this.c[i] * dx ** 2 + this.d[i] * dx ** 3; }}
// 使用例const x = [1, 2, 3, 4];const y = [2, 3, 5, 4];
const spline = new CubicSpline(x, y);console.log(spline.interpolate(2.5)); // 点 x=2.5 の補間値を計算console.log(spline.interpolate(3.5)); // 点 x=3.5 の補間値を計算4.双曲線補間
Section titled “4.双曲線補間”function hyperbolicInterpolation(x: number, x0: number, x1: number, y0: number, y1: number): number { const a = (y1 - y0) / (x1 - x0); const b = y0 - a * x0; const c = (x1 - x0) / (y1 - y0); const d = 1 / (y0 - a / b);
return (a * x + b) / (c * x + d);}5.線形補完
Section titled “5.線形補完”function linearInterpolation(x: number, x0: number, x1: number, y0: number, y1: number): number { return y0 + (y1 - y0) * (x - x0) / (x1 - x0);}